matematika mania: volume bola

memperoleh volume bola dimensi ke-n

Boleh dibilang ini adalah lanjutan dari postingan sebelumnya. Sekarang saya akan membahas bagaimana rumus volume bola dimensi ke-n diperoleh. Dinotasikan n-bola adalah bola pada dimensi ke-n dan $V_n(r)$ adalah volume n-bola dengan jari-jari $r$ , diasumsikan titik tengah bola berada di titik asal.

Konsep dasar untuk memperoleh rumus 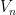$V_n$ sebagai berikut:

Potong n-bola menjadi potongan-potongan berbentuk n-cakram (cakram dimensi ke-n) dengan alas cakram berentuk (n-1) bola. Dengan kata lain kita bisa memandang n-bola tersusun dari n-cakram sebanyak n. Contoh:3-bola tersusun dari 3-cakram yang alasnya berbentuk 2-bola (lingkaran)
Hitung satu-persatu volume n-tabung kemudian jumlahkan semuanya untuk memperoleh $V_n$ .

Secara integral, konsep diatas dapat dirumuskan menjadi 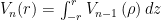$V_{n}(r)=\intop_{-r}^{r}V_{n-1}\left(\rho \right)dz$ dengan 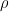$\rho$ adalah jari-jari n-cakram dan 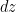$dz$ adalah ketinggian/ketebalan cakram

Hubungan $\rho$ dan $r$ adalah $\rho=r\sin\theta$ , selanjutnya kita ubah $V_{n}(r)=\intop_{-r}^{r}V_{n-1}\left(\rho \right)dz$ ke dalam koordinat polar .

matematika mania

Selasa, 04 Desember 2012

volume bola

memperoleh volume bola dimensi ke-n

Tidak ada komentar:

Posting Komentar